Unlocking the quantum code: Physicists map the statistics of entanglement
- FirstPrinciples
- Apr 1
- 4 min read
A new study maps all quantum correlations in the minimal Bell scenario, advancing our understanding of quantum entanglement and enabling universal, device-independent tests.
TL;DR: A new study has provided a complete description of the quantum correlations achievable in the minimal Bell scenario—two observers, two measurement settings each, and binary outcomes. This result sharpens our understanding of quantum theory’s boundary and lays the foundation for universal, device-independent tests of quantum systems.
A new look at quantum entanglement statistics
Quantum entanglement—where two particles become connected so that the state of one instantly influences the other regardless of distance—lies at the heart of quantum information science, underpinning advances in quantum computation, communication, and cryptography. Yet, despite its central role, the full structure of the correlations it produces remains an open question in many scenarios.
A new study published in Nature Physics by Victor Barizien and Jean-Daniel Bancal (Institut de Physique Théorique, CEA Paris-Saclay) addresses this challenge in the simplest meaningful experimental setup: the minimal Bell scenario. The authors provide a complete and exact characterization of the quantum statistics that can emerge when two observers each choose between two possible measurements with two possible outcomes—an experimental configuration that serves as a foundational test of quantum nonlocality.
Stay ahead of discovery—subscribe to FirstPrinciples Pulse for news and research in fundamental science, delivered straight to your inbox.
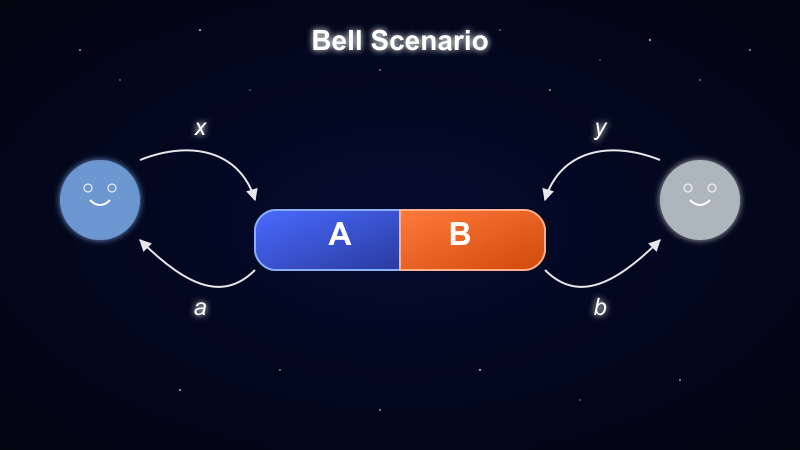
What is the minimal Bell scenario?
Imagine two researchers in separate labs miles apart, each with one particle from an entangled pair. A Bell test is an experiment where they independently choose which property of their particle to measure and then compare their results afterward. John Bell designed this test in the 1960s to determine whether quantum mechanics' strange predictions could be explained by some hidden, conventional mechanism we just hadn't discovered yet.
Quantum theory predicts correlations between measurement outcomes that cannot be explained classically—most notably, those that violate Bell inequalities. Such violation constitutes a “failure” of the Bell test, and indicates that the elements of the system are correlated in a way that violates local realism, which Einstein described as “spooky action at a distance”. However, not all nonlocal correlations are physically realizable. The quantum boundary—the full set of correlations allowed by quantum mechanics—has remained only partially characterized, especially when the shared state is not maximally entangled.
The simplest version of the Bell test is the minimal configuration, in which:
Each party chooses between two measurement settings.
Each measurement has two possible outcomes.
The shared quantum state may be partially or maximally entangled.
Prior to this study, even the minimal Bell configuration was fully described only for the case of maximal entanglement.
Physicists fully map quantum statistics in the minimal Bell test
Barizien and Bancal’s work achieves the first complete description of the quantum correlations possible in this minimal scenario. Specifically, they identify:
All quantum correlations that can arise from partially entangled two-qubit states, not just the maximally entangled ones.
The full set of self-testable correlations—those that determine the underlying state and measurements, purely from observed statistics.
Their method involves a novel mathematical transformation that connects the statistics of partially entangled states to those of maximally entangled ones. This yields a characterization of all correlations possible through quantum interactions in the minimal Bell configuration, enabling theoretical classification and practical application in quantum information protocols.
From theory to application: Impacts on quantum devices and foundations
Device-independent verification
Self-testing is a cornerstone of device-independent quantum information science. It enables one to certify the quantum state and measurements based solely on observed statistics—without relying on the internal workings of the devices. This work makes self-testing possible for a much broader range of scenarios, which, in turn, enables broader applications of device-independent quantum information.
Sharper theoretical bounds
By delineating the precise set of achievable quantum correlations, the study places tight constraints on the limits of quantum theory in this configuration. Any experimentally observed correlations lying outside this set would point to either experimental error or new physics beyond quantum theory. Crucially, these results hold regardless of the system used—whether photonic, superconducting, or trapped ion qubits—as they rely solely on observed statistics, independent of the internal workings of devices or the method of qubit encoding.
By building on this substrate-independent foundation, the work sharpens our understanding of quantum theory’s boundaries while providing a robust tool for validating quantum devices across platforms—reinforcing its dual value in both fundamental research and practical, device-independent testing.
Beyond Bell: future directions in quantum correlation research
This theoretical advance builds directly on recent experimental progress in quantum foundations, particularly the landmark Bell tests that earned the 2022 Nobel Prize in Physics. While those experiments offered compelling empirical evidence of quantum nonlocality, the present work provides a complementary theoretical contribution: a complete and exact characterization of the quantum correlations permitted in the minimal Bell scenario, laying a rigorous foundation for understanding the structure and limitations of quantum nonlocality.
Looking ahead, this framework opens the door to several promising avenues of research. One direction involves extending the characterization to more complex Bell scenarios that include additional measurement settings, outcomes, or entangled parties. Such generalizations would bring us closer to a comprehensive understanding of quantum correlations in more complex, multi-component systems. An open and intriguing question is whether similarly complete descriptions can be achieved for higher-dimensional or multipartite entangled states, which remain largely uncharted in current theoretical models.
The framework may also prove valuable in optimizing practical protocols for quantum communication, certified randomness generation, and cryptography—particularly in device-independent settings.
Toward a deeper understanding of quantum nonlocality
Barizien and Bancal's work represents a landmark achievement in quantum physics. This achievement not only deepens our understanding of quantum reality but provides practical tools for verifying and securing the quantum technologies that may transform computing, communications, and cryptography in the coming decades. As quantum computers continue to advance, this theoretical foundation helps ensure we can trust the quantum systems we build.
This article was created with the assistance of artificial intelligence and thoroughly edited by FirstPrinciples staff and scientific advisors.



