The biography of Nobel Prize-winning mathematician Roger Penrose will be published on November 12. Author Patchen Barss provided FirstPrinciples with a sneak peek.
In the world of mathematical physics, there are few names bigger than Sir Roger Penrose. His list of accolades — including a knighthood for his service to science and the 2020 Nobel Prize in Physics for the critical mathematical tools he proposed to describe black holes — are too many to list. At 93, as the Emeritus Rouse Ball Professor of Mathematics at the University of Oxford, he is still actively publishing new work.

The first biography of Penrose, The Impossible Man: Roger Penrose and the Cost of Genius, will be published on November 12 by Basic Books. Kirkus Reviews recently lauded its author, science journalist Patchen Barss, for his “superb insights into a flawed genius.”
Penrose is recognized as one of the most influential mathematicians, philosophers, and physicists of the last century, a man who routinely astounded colleagues with the elegance and beauty of his discoveries. In the excerpt below, Barss shares the story that catalyzed one such discovery, the eponymous Penrose triangle.
From The Impossible Man: Roger Penrose and the Cost of Genius:
He arrived late for a packed lecture by newly minted Fields Medalist Jean-Pierre Serre on the homotopy groups of spheres, only to discover the subject was impenetrable and the lecture was in French. He edged right back out the door, left the building entirely, and descended the stairs just as a tram pulled up. Off stepped British mathematician and code breaker Shaun Wylie. In his hand, he carried a catalogue from an exhibition at the Municipal Museum of Amsterdam. Roger and Shaun recognized one another and chatted on the street, catching up on the conference and common friends back in England.
Roger wasn’t really listening. He was transfixed by the catalogue Wylie held. The picture on the cover depicted bucolic black-and-white checkerboard fields, separating two villages that were near mirror images of one another. Each had a church, windmill, treelined streets, and rows of houses. Though part of the same scene, the lefthand village was sunlit, while night had fallen on the right.
As Roger’s eyes moved upward from the squares, the boundaries of the orderly fields at the bottom of the picture twisted and warped, morphing into the outlines of birds. On one side, the birds glowed white against the dark greys and blacks of the nocturnal scene. On the daylight side, they were black silhouettes on a white sky.
Where the flocks met in the middle, black and white birds interlocked seamlessly — each becoming the background of the other.
Roger couldn’t stop looking. He had seen many visual tricks and puzzles in his life, but nothing like this.
The catalogue came from an exhibition of Dutch artist M. C. Escher’s lithographs, which had been organized in conjunction with the mathematicians’ congress. Shaun pointed Roger toward the museum, which lay just across the Museumplein.
Escher’s prints amazed Roger. He had never seen anything so clever, so beautiful, so surprising and delightful. They were realistic and impossible at the same time. Escher played with perceptions of up and down, foreground and background, scale and dimension. The images were a revelation, yet also deeply familiar, as though the artist had reached into Roger’s own mind to pull out these ideas.
He stopped in front of a spectacular lithograph titled “Relativity.” Three black-and-white staircases approximated an equilateral triangle.
Platforms and smaller staircases connected the main flights, and arched doorways opened onto various idyllic gardens.
Abstract human figures moved through separate, overlapping worlds. Walls became floors, up became down, down became sideways.
Beings that seem nearly to touch as they passed occupied disconnected realities.
Each small section of the picture made perfect sense. But as Roger tilted his head one way and the other, “Relativity” became increasingly irrational. Up, down, and around the staircases, paradox piled on paradox. The image made powerful sense to him. Escher spoke in a visual mathematical language Roger understood fluently. The only other person he’d ever come close to sharing this language with was his father.
He spent the day awestruck and lost in the galleries. Interlocking birds turned into fish. Black and white humanoids stepped out of a two-dimensional image and marched around in circles to greet one another.
Lizards climbed up out of the page and over a dodecahedron before slinking back into their flat world. Tesseracts and collapsing spheres, distorting mirrors, conformal stretching. A subtle running joke about how all these creatures and objects that seemed to force their way into higher dimensions only ever existed on flat pieces of paper.
He returned to the conference with his own copy of the catalogue, more energized by the exhibition than by the talks of his fellow mathematicians.
Back in England, he travelled from Cambridge to London at his first opportunity to share the catalogue with Lionel [Penrose, his father], who was as fascinated as Roger. In his twenties, Roger still felt the rush when Lionel looked at him with interest.
They began creating their own “impossible objects.” They drew forests, roads, and streams, exchanging foreground and background and using perspective and two-dimensional trickery to create impossible scenes. They began with detailed, realistic images but quickly evolved toward simpler, more essentialised creations.
Each ultimately created one iconic stripped-down masterpiece, peeling away everything but the absolute essence of their illusions.

Roger borrowed the three-axis symmetry from “Relativity” to create the Penrose triangle. Each corner looked like a perfectly plausible sixty-degree angle formed of solid material. But something went wrong with the whole picture. Each of the drawing’s twelve lines was perfectly straight, but the sides of the triangle seemed to twist — the inside became the outside, and vice versa. The angles seemed to oscillate between sixty and ninety degrees. The Penrose triangle was irreconcilable with itself. Lionel, inspired by Roger’s triangle and Escher’s stairs, developed the Penrose staircase, four flights of stairs connecting the top edges of a seemingly rectangular tower. A person walking along those stairs would ascend (or descend) forever. The staircase had no beginning, end, top, or bottom.
…
Later that year, Lionel and Roger coauthored a short paper in the British Journal of Psychology (where Lionel was friendly with the editor), exploring the mental mechanisms behind their Escher-inspired impossible objects. “Each individual part is acceptable as a representation of an object normally situated in three-dimensional space; and yet, owing to false connections of the parts, acceptance of the whole figure on this basis leads to the illusory effect of an impossible structure,” they wrote.
Shrouding the Penrose triangle in abstruse academic language did not disguise its delicious simplicity: a child could sketch an impossible tribar, and yet its contradictions fascinated mathematicians and artists.
This paper, coming so early in Roger’s career, helped define him as a master of paradox and a creative thinker with appeal beyond the academic world.
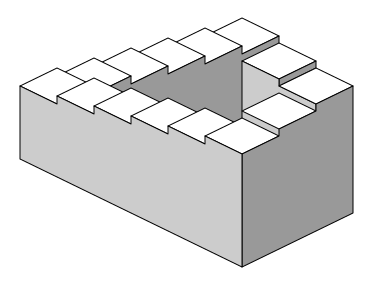
Lionel mailed the paper to M. C. Escher. “The triangle really belongs to my son, Roger, and the staircase was my contribution. We have a number of ideas which we wish you could illustrate because we are not clever enough to do this ourselves,” he wrote.
[Some years later] M. C. Escher took up Lionel’s exhortation to incorporate the Penrose triangle and the Penrose staircase into his lithography. “Waterfall” riffs on the impossible triangle. It depicts a cluster of buildings on a hilltop connected by a viaduct. Water spills over a central waterwheel, flowing back over two impossible tribars.
The water appears to move downhill but ends up back at the top.
Escher’s addition of detail and gravity turned Roger’s spare visual paradox into a perpetual motion machine. “Waterfall” became one of Escher’s most popular and iconic lithographs.
Roger felt more connected to the Dutch artist than ever. Examining a print of “Waterfall,” he noticed the geometric ornaments on top of the viaduct’s two towers. Each fused several regular polyhedra together, superimposing them at ninety- and forty-five-degree angles.
Those spiky, multifaceted gems looked very familiar to Roger — he had built these very shapes out of cardboard as a child, sitting on the floor with his father. The similarity was coincidental, but it fed Roger’s conviction that geometry was its own kind of reality. He and Escher — and Ted, Engelbert, Ivor, and others — were explorers, not inventors.
Excerpted from The Impossible Man: Roger Penrose and the Cost of Genius by Patchen Barss. Copyright © 2024. Available from Basic Books, an imprint of Hachette Book Group, Inc.



